Exponents and Radicals
Why Learn This Stuff?
When solving algebraic expressions, a solid knowledge of how exponents and radicals function is essential to the effort. A student without immediate recall of the results of common addition, subtraction, multiplication, and division operations quickly discovers that they are at a steep disadvantage to those who aren't lacking such skills. When faced with a current mathematics class assignment, not only do they have the current subject to learn, they have to trudge through elementary school math problems on top of the load they already bear. Often, there isn't time enough to finish the assignment because the simplest tools are not at their command. The understanding of the properties of exponents and radicals falls into the same category for any student studying algebra and beyond.The goal is to commit to memory the properties and operations described on this page. The best way to learn these is to work the examples shown and then practice multiple problems similar to them on your own. It is not rocket science, just rote work. But the time spent will be paid back to you many times over in higher grades and results that will be more accurate.
Properties of Exponents and Radicals
Radicals ARE Exponents
Well, kind of… actually the radical sign is just another way of representing an exponent. That is why both of these concepts are included together here. ANY time you see a radical sign, it can be replaced by an exponent. A plain radical sign as most often represented is nothing more than a symbol for the square root of what is under it. A square root is a number that when multiplied by itself, will return the base number.
Five is the square root of 25.
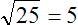
And when multiplied times itself, will return 25.
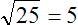
And when multiplied times itself, will return 25.
To represent the square root of a base number in a general case, we put the exponent
Property 1
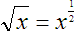
Sometimes though, a radical sign doesn't mean square root. If you see a tiny number, for example,
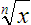 in the “V” part of the radical sign it is telling you that this expression represents a “root”
of the base number. It will be the
in the “V” part of the radical sign it is telling you that this expression represents a “root”
of the base number. It will be the
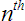 root of the base number. What does that mean? OK, let’s look at an example:
root of the base number. What does that mean? OK, let’s look at an example:
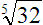
Here we see the base number 32 under a radical sign with a tiny “5” in the “V”. This expression means “the fifth root of 32”. That is to say, we are representing a number, when multiplied by itself 5 times over, will result in a product that is the base number. In this case, the answer is 2.
That leads us to the next property of exponents:
Property 2
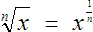
The
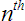 root of a base number is the same as the base number raised to the
root of a base number is the same as the base number raised to the
This is true when
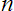 is a rational number.
is a rational number.
And if
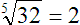 then we can go the other direction and state that
then we can go the other direction and state that
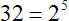 . Generalizing this concept, we have:
. Generalizing this concept, we have:
Property 3
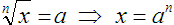
Where:
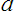 is either positive or negative, but never both if
is either positive or negative, but never both if
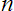 is odd.
is odd. 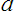 can be either positive or negative if
can be either positive or negative if
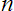 is even, but the principal
is even, but the principal
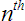 root is defined as even.
root is defined as even.- If
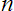 is even,
is even,
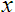 cannot be negative, unless you want to deal with imaginary numbers. E.g.
cannot be negative, unless you want to deal with imaginary numbers. E.g.
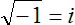
Now, if we reverse the positions of the terms in the equation in the example used in Property 2, we have
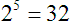 . This illustrates yet another property.
. This illustrates yet another property.
Property 4
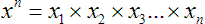
For
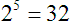 , we would have
, we would have
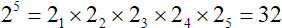 .
.There will always be exactly
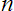 factors. This property is limited to whole-number exponents.
factors. This property is limited to whole-number exponents.
Well then, what if we find an exponent of zero? What does that mean? By definition:
Property 5
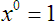
There is controversy in the case where
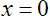 .
Some argue that
.
Some argue that
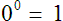 .
Some argue that it is undefined. Pick whichever side you like.
(I like the answer that
.
Some argue that it is undefined. Pick whichever side you like.
(I like the answer that
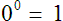 .)
But ANY non-zero number raised to the
.)
But ANY non-zero number raised to the
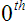 power is 1. (Not really considered a property per se, but good to know also, is that
ANY number raised to the power of one is itself:
power is 1. (Not really considered a property per se, but good to know also, is that
ANY number raised to the power of one is itself:
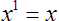 ).
).
Now let’s consider negative exponents. Yes, we can give a number a negative exponent. What does that mean? Let’s look at an example:
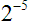
All this is really saying is that it is 2 raised to the fifth power, but in the denominator of a fraction. It is telling us to take the reciprocal of
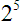 .
Generalizing this gives us yet another property:
.
Generalizing this gives us yet another property:
Property 6
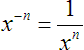
This property is always applicable except that
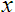 can never equal zero. That would cause the fraction to be undefined.
can never equal zero. That would cause the fraction to be undefined.
One final property we want to define here deals again with fractional exponents. We should already be aware that a positive integral exponent indicates we are raising a base number to some power. And we have seen that an exponent of ½ is given to represent the taking of the square root of the base number. But what about other fractions? What would
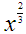 mean, for instance?
mean, for instance?
If you study the fraction,
The order in which this math is done is not important. The same answer will be forthcoming. To put this into a general case, we present this final property:
Property 7
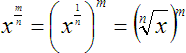
Or, because as was stated earlier, the order of operation will not change the answer:
.gif)
Simultaneously raising a base to a power and taking a root of it is represented by applying a fractional exponent. This exponent can be greater than or less than unity.
Gathering all the properties into one location for convenience, we have:
Property 1
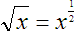 Sometimes the radical will have a tiny 2 in the ‘V’ of the symbol
Sometimes the radical will have a tiny 2 in the ‘V’ of the symbol
Property 2
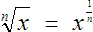 When
When
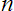 is a rational number
is a rational number
Property 3
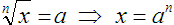 If
If
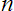 is even,
is even,
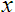 cannot be negative or the result is imaginary
cannot be negative or the result is imaginary
Property 4
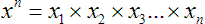
Property 5
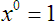
Property 6
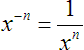
Property 7
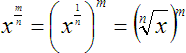
or
.gif)