Figuring a Square Root By Hand
Can you calculate a square root by hand? No, no, no, I don't mean you specifically, at least not yet. I mean can it be done? Yes it can! It isn't very hard and when the feat is performed it will make you (yes, now I do mean you) look extremely geeky in front of your friends.Do we need a secret calculator? Nope. Do we need a slide rule (a WHAT? - Hey, if ya gotta ask, don't worry about it.) Anyway, again, nope. Well, how about an abacus? No, we do not need any artificial tools; all we need is a pencil, a piece of paper, and your brain.
Why would anyone want to know how to calculate a square root the way they used to do it a hundred years ago or more? I dunno... Why would anyone want to know how to start a fire without matches? Why would someone want to be able to tell the weather without turning on the TV?
I suppose I could make up something profound like, "Well if you got picked to be on one of those TV shows where you were dropped off in the back corner of some godforsaken desert, you'd sure be glad to know how to calculate a square root by hand, by golly!". But I won't insult your intelligence. The only real reasons to become skilled at this task are:
- Because it can be done, and
- You will be one of a very small (indeed, VERY small) population that will hold the ability to perform this amazing technique.
What is the square root of 77,789.65? (Oh come ON now, you didn't think we were going to try to take the square root of 64 or 16 or 4 did you? You did? What fun would that be? And you wouldn't learn anything that way either.) Alright let's get down to learning the lost art. Pencils ready? Follow along and you will see...
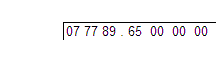
I know, I hear you saying, "Hey! That looks like a division problem! And you stupidly put an extra zero at the front of the number that isn't supposed to be there! What's with all the extra zeroes? Where's the square root demo you promised?"
Calm down, this is how we start. But if you look a little more carefully, or maybe you already have, you can see that we took 77,789.65 and spaced it out a little in groupings of two digits. With any number you start at the right and group the digits into sets of two. The extra zero at the front is to make the number of digits in the number become even rather than odd.
It looks a bit different than division now doesn't it? No, not yet? Well, trust me, it will.
OK, yes, there is a resemblance to division here. But it is a different process. We work with these digits in groups of two. Here we start with "07". We ask ourselves, "What is the largest square of a number we can subtract from 7 and still have a positive remainder?" How about "2"? Yeah, 2 squared is 4 and we can subtract that from 7 and still have a positive number left over.
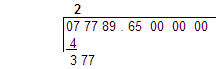
So we put 2 on the top of the bar and put its square, 4 under the 7. Perform simple subtraction, (7 - 4) and we get 3. Put the 3 under the 4, then bring down the next two digits from the number we are trying to get the square root of, in this case "77".
Now for something new. OK, out to the left of our work, on the next line below our current "377" sub-answer we put the double of the number we have on the top line. Here we double 2 and put 4 there. But next to it we need to put a question mark (temporarily).
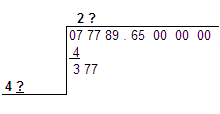
You will notice there is a question mark to the right of the 2 on the top line as well. Why? Well, both those question marks are place-holders for the same digit. What digit you ask? Good question, and the right one too!
The digit we need is the largest one that when put there will make [ (4*10) + "?" ] * "?" <= 377. How about an example? (I know, you thought I'd never offer...)
What if we multiplied 43 * 3? We'd get 129. We could subtract that from 377 and get a positive remainder. But 43 * 3 will not be the biggest number we could find without going over. Well, if the number was simply 40, that would go into 377 9 times. But 49 times 9 is 441 and is too big. Let's try 47 * 7. That is 329, and turns out to be the correct choice!

So we put the 329 directly under the 377, make our subtraction and get 48. Then just as we did last time, we bring down the next two digits; here those will be "89". Replace both the question marks with 7s, and we're ready to move on.
Just as we did in the last round, we look at the number we have above the line (here it is 27) figure what double that number is (that'd be... hmm.. let's see here... 54!) and put that doubled number on a line out to the left and below the last number we calculated. Again, we put a question mark as a place holder after that number and on the right hand side of the number we have on top of the line.
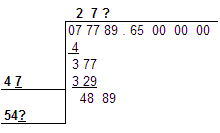
The question marks both need to be the same digit. And after replacing them with that same digit the resulting numbers have to be able to be multiplied together and be less than or equal to 4889. OK, we already have a number that is going to be five hundred forty something. You can probably ballpark how many times 540 would go into 4889. Likely, 8 is what I'd start with for our purposes. Because even though 540 times 9 is less than 4889, it isn't much less. And I know if I tried 549 times 9, we'd be way over. So what is 548 times 8? It is 4384. Let's see how that fits in our problem here...
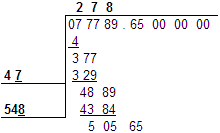
Yes, it works well! So, now we subtract it from our last result and get the answer. Bring down the next two digits and we are ready for the next round.
Remember, the next step? Yes, very good; look at the number written above the line, 278, double it (that is 556) and write that new number to the left on a new line below the last calculated answer. Now that you have seen this a couple of times, we are going to dispense with the question marks. You understand that we need to add a final digit to the end of our number on the left line and we need the same digit on the top line at the end of that number. Also the full number on the left line (556?) must be able to be multiplied times that final digit on the top line (?) and still be less than the calculated result from our last step (50565). That digit works out to be 9 and the result of using it is just below this paragraph. We are going to put the decimal point into the number on the top line, because it ultimately will be needed there. But it will not impact our calculations in any way.
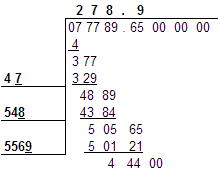
Not too hard is it? Most of the time, no. But there are twists occasionally. And we are coming up on one here. (No, don't get scared! it will be understandable, and it is rather reminiscent of a division problem when the same issue is encountered.)
So we did our math and multiplied 5569 times 9 and got 50121. We subtracted that from 50565 and got 444. We then brought down our next two digits 00 to give us 44400. Now, per the rules, we need to take the number on the top of the line 2789 (ignore the decimal point for now) double it to 5578, put 5578 on a line to the left and below our last answer, and leave the space after the 5578 open for the next digit.
Now we are going to try to figure out how many times fifty five thousand seven hundred eighty something has to be multiplied times some number to get forty four thousand four hundred. OMG! Can't be done, can it? Not and be one or larger it can't!
But, don't fret; where there's a will there's a way! Put a zero on the top line. This just means we multiply 0 times 55780 and get 0 to subtract from 44400. See, told ya this part was kinda like a division problem. You've seen this before. Maybe a long time ago, but I assure you, it was taught in your 5th or 6th grade math class!

Then we calculate the answer, 44400, bring down two more digits, 00 and we have 4440000. Now just more of the same as we have been doing. Double the top, put it on the left, knowing we need one more digit to finish that number and that that same digit will go on the top. Figure out the largest digit that will give us a number smaller than the one we are trying to subtract from after we multiply it times our left side number...etc.

The last iteration we are going to pursue gives us this:

Looks pretty impressive, doesn't it? Did we waste a bunch of time doing this? Well that depends on how you define wasting time. Could it have been done faster? Yes, a calculator will do this lightning fast. But if you are asking, "Did we get a meaningful answer?", the response is unequivocally, "Yes!"
Now the fun part - Multiply 278.9079 times itself. (OK yes, after all that math it is time to let your brain cool off. Go get a calculator and poke in the digits, unless you just love manually crunching numbers.)
What'dya get? I got 77789.6167. Disappointed it isn't exactly the same as our manual work? Don't be! You too can get calculator precision results if you want to continue to pound on this problem.
You see, it is just a matter of precision. Do this: Put 77789.65 into your calculator and hit the square root button. And...the answer is... 278.9079597 is what I get. So you see, if you keep going, you will tie out to the calculator eventually. You stop when you get a number that is accurate enough for your purposes or until you feel your head is about to explode.
We'll leave this lesson with a worthwhile quotation (whose I haven't the vaguest notion): "Use it or lose it." That phrase applies specifically to this problem, but also to almost anything we ever learn. You WILL forget how to do this unless you practice it now and again.
If you plan on impressing someone with your newfound knowledge here, take out a piece of paper a few minutes or hours beforehand and make sure you can really still do it. I know first-hand about this. I had the big "Duh..." moment as I started on this web page. But a little practice and I'm good again for a few weeks.