| Physics - Chapter 3 |
| Section 3-6 -
Problem 29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Problem 29: |
|
|
|
|
|
|
|
|
|
|
|
| In hot pursuit, Agent Friday* must get directly across a 1600 m wide river in the
minimum amount of time. The river
current |
|
|
| is
0.80 m/s. Friday can row a boat at
1.50 m/s and can run at 3.00 m/s.
Describe the path Friday should take, rowing |
|
|
| plus running
along the shore, and determine the minimum total time. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
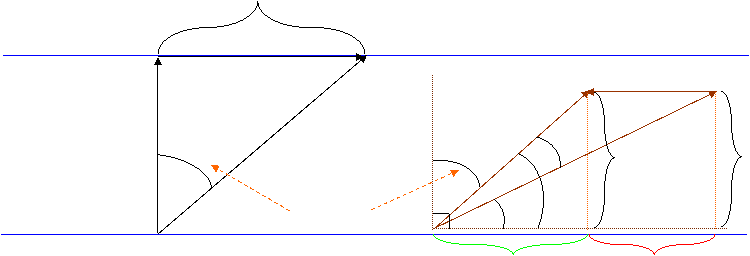
| We
start by diagramming out the stated problem.
The diagram actually has to be drawn in two separate sections. That is
the trick |
|
| to this
confusing problem. We need to point the boat (presumably UPstream) along vector VBW at the angle γ relative to |
|
|
| the shore.
The current pushes downstream along vector VWS. These act to create
the resultant vector VBS. This is the motion |
|
| of the boat
with respect to the shore. This
relationship is drawn in the right hand side of the diagram below. These are
velocity |
|
| vectors. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| The angle VBS makes with a line straight across the river is identical
to the angle that the boat will be traveling as it crosses the river. |
|
| That angle is
θ. VBS will give us the velocity the boat would travel along
angle θ. And having calculated angle θ we can determine the |
|
| length of
vector X. Knowing the
distance, and having previously calculated the velocity, we can then figure
out the length of time that |
|
| traversing
the river would take. And again, knowing the angle θ we can calculate
the length of vector D. And knowing that the length of |
|
| vector D would be traveled at
3.0 m/s, we can then calculate the time necessary to traverse it. These
relationships are |
|
|
| diagramed
in the left side and are illustrated in the displacement vector set. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Displacement Vectors |
|
|
Velocity Vectors |
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
VWS |
|
|
|
|
→ |
|
|
→ |
|
|
→ |
|
current |
|
|
|
|
R |
|
|
X |
|
|
VBS |
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
VBW |
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
θ |
|
|
|
θ |
|
|
VBSy |
|
VBWy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
Same angle |
|
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VBSx |
|
VWSx |
|
|
|
Note: Cells highlighted in blue are input areas
and may be |
|
|
|
|
|
|
|
changed. Cells highlighted in yellow are
results and should |
|
|
|
|
|
|
|
not be altered. |
|
|
|
|
|
|
VBWx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Displacement Vectors |
|
|
|
Velocity Vectors |
|
|
|
|
|
→ |
Distance
directly across River |
|
|
→ |
Velocity of Water with respect to the Shore |
|
|
R |
1600 |
m |
|
|
|
VWS = |
0.80 |
m/s |
|
|
|
|
→ |
Distance across river at angle θ to straight across |
→ |
Velocity of Boat with respect to the Water |
|
|
X |
1618 |
m |
|
|
|
VBW = |
1.50 |
m/s |
|
|
|
|
→ |
Distance to be covered on foot |
|
|
→ |
Velocity of Boat with respect to the Shore |
|
|
D |
243 |
m |
|
|
|
VBS = |
1.39 |
m/s
at |
-8.6 |
° from straight across |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Steps: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Given γ in
degrees: |
66.8 |
The
boat is pointed |
23.2 |
° Upstream |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
Calculate VBS: |
|
|
|
|
|
The sum of the two known vectors will give us |
|
|
→ |
|
→ |
|
→ |
|
the vector that the boat has relative to the
shore. |
|
|
VBS |
= |
VBW |
+ |
VWS |
|
We work this by extracting the x and y
components |
|
|
|
|
|
|
|
|
of the known
vectors. |
|
|
|
Calculate VBWx: |
|
|
|
Calculate VBWx: |
|
|
|
|
|
|
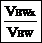
|
|
|
|
|
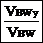
|
|
|
|
|
|
|
|
cos γ = |
|
|
|
|
sin γ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VBWx = VBW * cos(γ) |
|
VBWy = VBW * sin(γ) |
|
|
|
|
VBWx = |
1.50 |
0.394 |
m/s |
|
VBWy = |
1.50 |
0.919 |
m/s |
|
|
|
|
VBWx = |
0.59 |
m/s |
|
|
VBWy = |
1.38 |
m/s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VBSx = VBWx + VWSx |
|
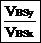
|
|
|
|
|
|
|
|
VBSx = |
0.59 |
-0.80 |
|
|
tan α = |
|
|
|
|
|
|
|
VBSx = |
-0.21 |
m/s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.38 |
|
|
|
|
|
|
VBS = |
|
tan α = |

|
= |
-6.59 |
|
|
|
|
|
|
|
-0.21 |
|
|
|
|
|
|
VBS =[ ( |
-0.21 |
) 2 + ( |
1.38 |
) 2 ] 1/2 |
|
|
|
|
|
|
|
|
VBS = |
1.39 |
m/s |
|
|
atan ( tan α) = |
98.6 |
Degrees |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Theta becomes: |
|
|
|
|
|
Now we have the velocity and angle that the
boat will |
|
θ =
90° - α = |
-8.6 |
Positive is degrees upstream |
|
have as it travels across the river. We will
use those |
|
|
|
degrees |
Negative is degrees downstream |
|
in our displacement calculations. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Now knowing the angle theta, we can calculate
our displacement vector lengths: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
→ |
|
|
|
|
|
|
|
Calculate
X: |
|
|
Calculate |
D: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
R |
|
|
→ |
|
|
|
|
|
|
|
|
X = |
|
|
|
D = |
R * tan(θ) |
|
|
|
|
|
|
|
|
cos(θ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
→ |
1600 |
m |
|
D = |
1600 |
* |
-0.152 |
|
|
|
|
|
X = |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.989 |
|
|
Positve is upstream of directly across,
negative is downstream |
|
|
|
→ |
|
|
|
→ |
|
|
|
|
|
|
|
|
X = |
1618 |
m |
|
D = |
-243 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculate
T1
: |
|
|
|
Calculate
T2 : |
|
|
|
|
|
|
This is the time the boat takes to cross the
river. |
This is the time spent running down the shore. |
|
|
|
T1 = |X| / VBS |
|
|
|
T2 = |
|D|
/ 3.0 m/s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 = |
1618 |
/ |
1.39 |
|
T2 = |
242.6 |
/ |
3.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 = |
1161 |
s |
|
|
T2 = |
81 |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculate Total Time: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 + T2 = |
1241 |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pointed Upstream (Degrees) |
T1 |
T2 |
T1+T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-10 |
|
|
1083 |
383 |
1466 |
|
|
|
|
|
|
|
-5 |
|
|
1071 |
332 |
1403 |
|
|
|
|
|
|
|
0 |
|
|
1067 |
284 |
1351 |
|
|
|
|
|
|
|
5 |
|
|
1071 |
239 |
1310 |
|
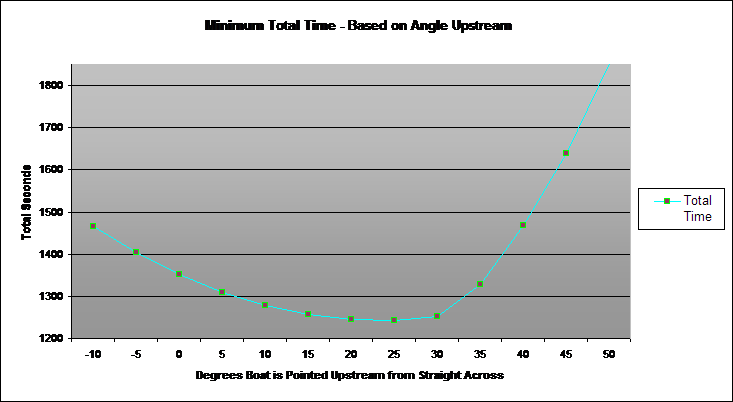
There may well be other ways of calculating the |
|
10 |
|
|
1083 |
195 |
1278 |
|
minimum time by building an equation that
relates |
|
15 |
|
|
1104 |
152 |
1256 |
|
γ and θ, but that is not
the method used here. |
|
|
20 |
|
|
1135 |
109 |
1244 |
|
After trying a few numbers to get a ballpark
range |
|
25 |
|
|
1177 |
65 |
1242 |
|
we constructed a graph using this workbook's |
|
30 |
|
|
1232 |
21 |
1253 |
|
algorithms to determine total time vs. the
angle |
|
35 |
|
|
1302 |
26 |
1328 |
|
that
the boat was pointed upstream. |
|
|
40 |
|
|
1392 |
76 |
1468 |
|
|
|
|
|
|
|
45 |
|
|
1508 |
131 |
1639 |
|
|
|
|
|
|
|
50 |
|
|
1659 |
193 |
1852 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pointed Upstream (Degrees) |
T1 |
T2 |
T1+T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
1135.123 |
108.582 |
1243.705 |
|
|
|
|
|
|
|
20.2 |
|
|
1136.574 |
106.858 |
1243.432 |
|
|
|
|
|
|
|
20.4 |
|
|
1138.042 |
105.133 |
1243.176 |
|
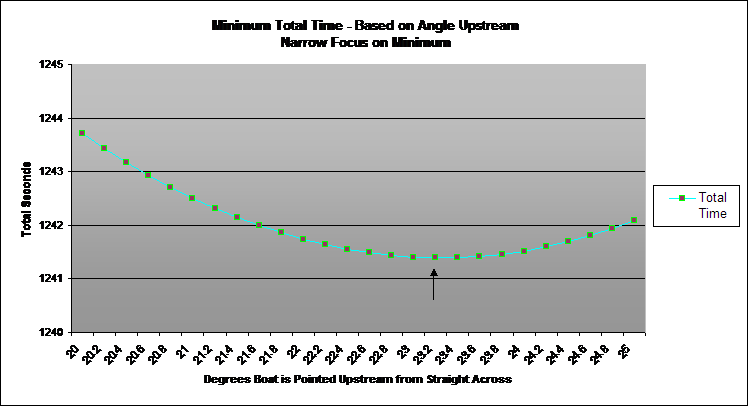
Then we further refined the graph by zooming in
to |
|
20.6 |
|
|
1139.529 |
103.407 |
1242.936 |
|
the range where we knew
the answer would be. |
|
20.8 |
|
|
1141.033 |
101.681 |
1242.714 |
|
|
|
|
|
|
|
21 |
|
|
1142.555 |
99.954 |
1242.508 |
|
The ultimate answer is
to point the boat 23.2 |
|
21.2 |
|
|
1144.095 |
98.226 |
1242.32 |
|
degrees
upstream of straight across. |
|
|
21.4 |
|
|
1145.653 |
96.496 |
1242.149 |
|
This grounds the boat on the opposite shore |
|
21.6 |
|
|
1147.229 |
94.766 |
1241.995 |
|
227 m downstream of straight across. Then |
|
|
21.8 |
|
|
1148.824 |
93.035 |
1241.859 |
|
Friday runs the remaining distance for a total |
|
22 |
|
|
1150.437 |
91.303 |
1241.74 |
|
elapsed time of 1241 s. |
|
|
|
22.2 |
|
|
1152.069 |
89.569 |
1241.638 |
|
|
|
|
|
|
|
22.4 |
|
|
1153.719 |
87.834 |
1241.554 |
|
The workbook has been saved with the correct
angle |
|
22.6 |
|
|
1155.389 |
86.098 |
1241.487 |
|
to arrive at the final answer. |
|
|
|
22.8 |
|
|
1157.077 |
84.361 |
1241.438 |
|
|
|
|
|
|
|
23 |
|
|
1158.784 |
82.623 |
1241.407 |
|
|
|
|
|
|
|
23.2 |
|
|
1160.511 |
80.883 |
1241.394 |
|
|
|
|
|
|
|
23.4 |
|
|
1162.257 |
79.141 |
1241.398 |
|
|
|
|
|
|
|
23.6 |
|
|
1164.022 |
77.398 |
1241.421 |
|
|
|
|
|
|
|
23.8 |
|
|
1165.807 |
75.654 |
1241.461 |
|
|
|
|
|
|
|
24 |
|
|
1167.612 |
73.908 |
1241.52 |
|
|
|
|
|
|
|
24.2 |
|
|
1169.437 |
72.160 |
1241.597 |
|
|
|
|
|
|
|
24.4 |
|
|
1171.281 |
70.411 |
1241.692 |
|
|
|
|
|
|
|
24.6 |
|
|
1173.146 |
68.660 |
1241.806 |
|
|
|
|
|
|
|
24.8 |
|
|
1175.031 |
66.907 |
1241.938 |
|
|
|
|
|
|
|
25 |
|
|
1176.936 |
65.152 |
1242.089 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* The Physics book used a different name for
the agent. I used "Friday"
in honor of the great sci-fi writer Robert Heinlein |
|
|
whose
story "Friday" was one of my favorites. Friday in Heinlein's book was an agent
extraordinaire. Where better to invoke |
|
her
presence than in a problem such as this one? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|