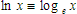Logarithms - A Primer
Why We Are Here
When originally introduced to logarithms in high school, I was mystified. They appeared to be something like those other mysterious creatures, "sin", "cos" and "tan". They all are bunches of letters that look like they might be treated as variables, but they are not. What we are here for today is to try to demystify logarithms by:- Explaining what they are
- Showing some rules for their use
- Providing detailed examples
- Plugging in real numbers for clarity
What Are These Complex Beasts Called "Logarithms"?
Are they really complex? Well, I suppose it depends on how they got explained to you. There are rules for their use. However, doesn't most everything in math have rules? I think what it comes down to is if you understand what logarithms are supposed to represent, it is easy to remember how to work with them. Why? Because a logarithm is essentially another way of looking at some number raised to some power.You know about powers, right? Exponents, little superscripted numbers above and to the right of some bigger number? For example, we all know that 102 = 100. All that is saying is multiply ten by itself once and you get one hundred; 10 times 10 equals 100. Logarithms do the same thing, but kind of in reverse.
Reverse? How so? OK, let's take a look at the same 10 x 10 problem, but presented as a logarithm.
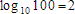
This equation is read as, "The logarithm, base ten, of the real number one hundred equals 2". You see? The "logarithm" is actually the answer to the problem. It is the number two. And as we saw earlier and already knew, that same two is the power or the exponent to which we had to raise ten to get 100.
What that says is that a logarithm is nothing more than an exponent. What makes it confusing is that logarithms present the numbers we are used to seeing in an unfamiliar context or order. When we see a logarithmic problem, we are in effect being asked to back into the answer. And the way I find it easiest to interpret the problem is to see it as asking me, "To what power do we need to raise the base 10 to get the answer 100?"
So, when presented with a logarithm problem that looks something like this:
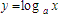
simply rearrange it in your mind to look like this:
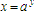
Figure out how to solve for the exponent and your work is done.
Now, to answer the question that heads this section, I will tell you that logarithms are exponents or powers. They are called logarithms because every group of insiders (in this case mathematicians, scientists and engineers) like to have a jargon to make themselves sound more impressive. You need to "savvy the lingo" to be with their "in" crowd.
What's that you say?...that isn't what you heard? Yes, I know Wikipedia has a much more technical explanation. But I do not have to subject this website to "[citation needed]" scoldings, so I can opine my irreverent musings on word meanings. (Actually, the Wikipedia website is excellent and I highly recommend you visit it... once you have completed this tutorial on the subject.)
Why Would Anyone Want to Twist A Simple Equation Into Something Complex to Find an Exponent?
And a good question this is indeed! The reason why is that it can be easier to solve many problems if you work with their logarithms rather than the numbers themselves. At least it used to be a lot easier and faster. When all we had were slipsticks (more jargon for you - read this as "slide rules") and log tables, logarithms vastly simplified calculations. Now with hand calculators that would best the fastest Cray supercomputer of the 70's, logarithms have fallen into a state of lesser use. But they still are quite important to understand.I believe I will leave much of the detailed information about how and why logarithms are used for other websites to explain. What we are aiming for here is to be able to understand what logarithms are and how to manipulate them.
Basic Logarithmic Properties
There are a number of properties that logarithms have that allow you to work with them and calculate answers. Let's look at these properties here.Multiplicative or Products Property
This is the equation for the Multiplicative or Products Property:
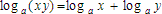
It says that when you take the logarithm of two numbers multiplied together, it will equal the sum of the logarithms of the two individual numbers. Let's put some numbers to this to make it a bit clearer:
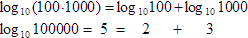
What it does not say is that the logarithm of two numbers multiplied together is equal to the two logarithms multiplied together. This point is one where it is easy to get confused. The next illustration should make very clear what to do and not to do. (You can click on it to enlarge it:
Divisive or Quotients Property
This is the equation for the Divisive or Quotients Property
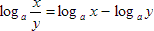
It says that when you take the logarithm of one number divided by another, it will equal the difference of the logarithms of the two individual numbers. Let's put some numbers to this to make it a bit clearer:
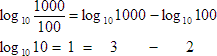
What it does not say is that the logarithm of one number divided by another is equal to the quotient of the two logarithms. This point is another where it is easy to get confused. Again an illustration is provided that should make very clear what to do and not to do. (You can click on it to enlarge it:
Powers or Exponents Property
This is the equation for the Powers or Exponents Property
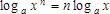
It says that when you take the logarithm of the nth power of a number it is equal to n times the logarithm of the number. Let's put some numbers to this to make it a bit clearer:
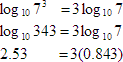
"Other" Properties
The logarithm in any base of the number one is zero.
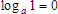
Here is a simple numeric example that should look familiar:
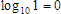
The logarithm in any base of the base number itself is one.
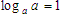
And here again, is a simple numeric example that should look familiar:
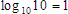
Now that we have seen the basic properties of logarithms, let's see what we can do with them.
Base Changing
Most of what we have been working with here are logarithms set in base 10. I.e., we are using the number 10 and are raising it to various powers. These are called "common logarithms". There is nothing particularly special about 10, however. Probably because humans have ten fingers, base 10 seemed like a good idea. And since everything else was base 10, why not our logarithms?So, can logarithms work in other bases? Sure they can! Remember, a logarithm is really nothing more than a power that you raise some base to. We can raise any number to any power we want to. And all the concepts in this page are applicable to logarithms in any base.
So, how do you get from one base to another? This next illustration shows how the conversion equation is derived.
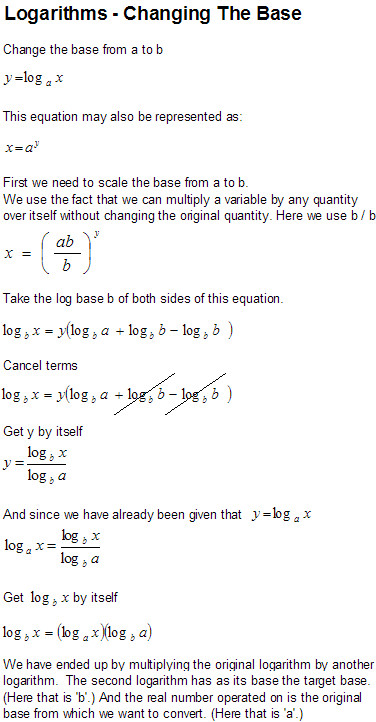
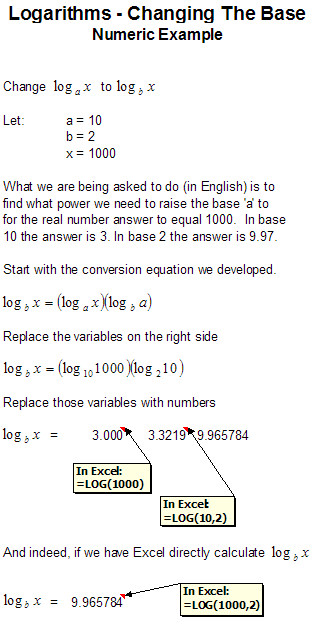
Now, as promised above, we will put some actual numbers into this equation to show how it is used.
Final Points Here
We'll leave this discussion after one more piece of information. As stated above, logarithms in base 10 are "common" logarithms. However, although they are common, they are not the most used in science and engineering. There is a much more extensively used base. And it is called "e"."e" is approximately equal to 2.71828. It is one of the most important concepts in all of mathematics. The function "e raised to the x power" has the same value as the slope of the tangent line for all values of x. Here again, I will suggest as a starting point the Wikipedia page on e as I can in no way provide a better explanation.
That said I'll leave you with this. When e is used as the base for a logarithm, the logarithm is called the "natural logarithm". It is represented with a preface of "ln" rather than "log" as we have used for the common logarithms.