Simpson Microammeter Internal Resistance
How Much Does This Thing Load a Circuit?
The meter being tested here is not anything special. It is an old Simpson 50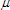
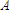DC ammeter.
I use it to monitor the signal strength of stations
I listen to on my crystal radio. But I became interested in trying to determine, as accurately as possible, the internal resistance of the device.
I learned earlier this year (2009) when I was testing a "joule thief" circuit, that a supposedly low resistance ammeter would markedly affect the circuit I was working with, to the point that I had to come up with a better measurement tool. (That tool turns out to be, put a 1
resistor in series in the circuit and test the voltage
drop across it. More on that in another page.) I wondered just how much resistance was being presented to a circuit by an ammeter.
Although I did my "joule thief" testing with a digital ammeter, and I did try to come up with a rough idea of the internal resistance for it, I wasn't convinced that I was really calculating out the correct value. So I put those numbers aside and pulled out the analog Simpson meter to make a solid attempt at finding its internal resistance.
The Methodology
The circuit for testing this is simple. A resistor is put in series with a dry cell and the ammeter. The value of the resistor is chosen such that the voltage source will drive the meter to exactly full scale deflection, and no more. I had handy a rechargeable Ni-Cad cell with a voltage of 1.296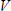
. I needed to drop the current to
50.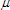
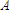I calculated I should need around 26k.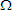
I did not want to break the meter by putting in too little resistance to start. I put into the circuit my Cornell-Dubilier RDA-RDB-RDC Resistance Box and set it to 30k
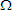. This, as expected, was too
much resistance. As I adjusted the dials, I ended up with 23.1k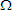
as the indicated resistance. I pulled the resistance box out and put in several resistors that came close to the 23.1k
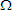value. When I connected the power to the circuit again,
I could see that this had worked. The meter's needle was on "50" as closely as I could read it.
The next step should have been simple. Put a shunt resistance in parallel with the meter to drop the current through it to exactly one half scale. I did this, once again using the resistance box to select the correct resistance. It was 1780
.
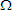Two things about this surprised me. First was that the resistance was so high. (Although it was in the ballpark with that I had calculated for the digital ammeter.) And second was that when I tried to tie all the measured numbers together, I was not exactly on target. Oh, yes, they were pretty close. And I knew that this number must be representative of what the resistance actually was. But I wanted a more convincing set of calculations. I also pulled out my Shallcross 638-R Kelvin Wheatstone Bridge to make certain of the resistances. This device can measure resistances at an accuracy level of 0.3% between 1
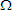and 1 M.
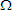After using it here, I am a believer.
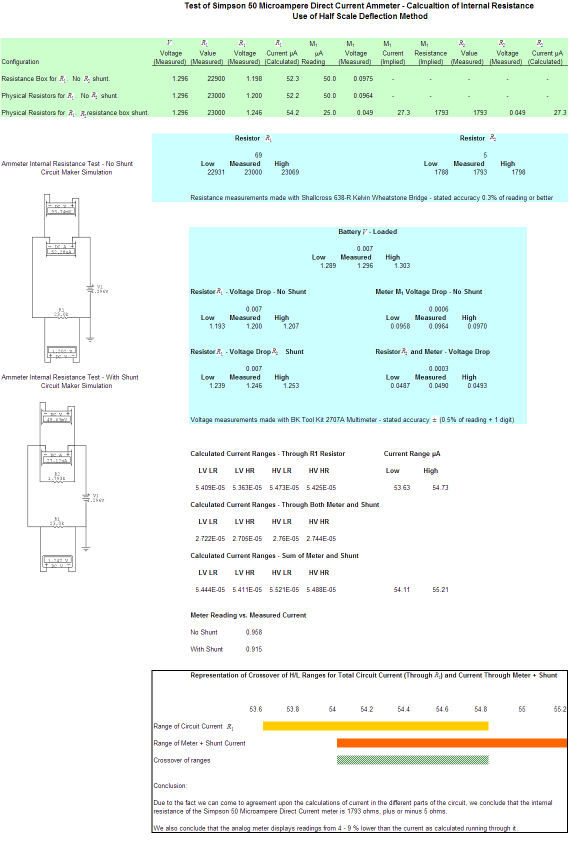
The graphic below may be clicked upon to enlarge it. This is the results of the experimentation as captured in an Excel workbook. I am not going to repeat the stuff I have shown below as the workbook should be self-explanatory, with a little study.
Excel Workbook Calculations and Results
)
Click picture to enlarge
Conclusion
The ammeter has 1793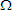 internal resistance. The numbers
in the workbook confirmed that to my satisfaction. Interestingly, the meter seems to read around 4-9% low when the circuit current is measured
externally, as was done here.