Ohm's Law
Voltage, current and resistance are all related in an electrical circuit, whether it is AC or DC. For the DC circuit, Ohm's Law can be described by a simple formula tying the three parameters together.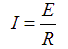
"I" is the current in amperes. If we think of electricity as water then we can consider current to be like the rate that water flows down a stream.
"E" is the pressure or electromotive force in volts. Again using water as an analogy, volts are like pressure that water has behind a faucet. If you turn the faucet on and a trickle comes out that you can stop by plugging your finger into the end, it is low pressure. If the flow cannot be stopped, you would consider it high pressure.
"R" is the resistance in ohms. Once again, making a comparison to water, we could consider a large pipe as having low "resistance" to the flow of the water as it may let as much as is available through. Then a small pipe would constrict the flow and offer a higher "resistance" to the water flow.
There are two other ways that the Ohm's Law formula can be algebraically manipulated. Each of "E" and "R" can be set standalone on the left side of the equation. These permutations look like this:
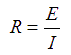
and
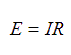
All three versions are used extensively throughout electronics.
Let's look at a few examples of the way these formulas work:
First we have to make sure that we are using the correct units when making our calculations.
- Current or "I" is often reported in milliamperes or microamperes. These must be converted to basic "amperes" for use with Ohm's Law.
- Resistance or "R" may be described for example, in kilohms or megohms. But to use Ohm's Law, these units must be converted to the base "ohms".
- Voltage or "E" can be described (among many other terms) as millivolts or kilovolts. Again, to use these formulas, we must have these reported in the basic unit "volts".
How do you convert back and forth between these units? Electronics uses the metric system and so has standard prefixes that mean the same regardless what they are used for. Kilo is 1,000, - Mega is 1,000,000 - Micro is 1/1,000,000 - Milli is 1/1000. There are many more and that is the subject for another page. You can find those terms and plenty of others here.
You must know two out of the three variables in order to calculate the third. Let's start with a very simple circuit. In this circuit we know R and E, but need to find I.
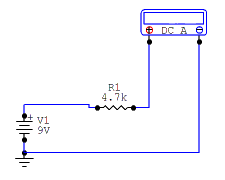
Here we can see the Resistance is 4.7k ohms and there is a battery supplying 9 volts DC. The voltage is in the correct units, "volts" but the resistance is not. When you see k ohms it simply means 1000 ohms. So, 4.7k ohms is 4700 ohms.
When we put these numbers into the first version of Ohm's Law it looks like this:
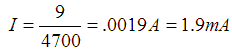
9 volts divided by 4700 ohms = 1.9 mA.
Next we are given a similar circuit, but this time the resistance is unknown:
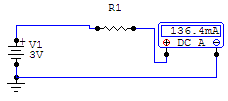
When these numbers go into Ohm's Law (the second variation) it looks like this:
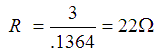
3 volts divided by .1364 amperes = 22 ohms.
And now we see a circuit where we are given the resistance and the current but not the battery voltage:
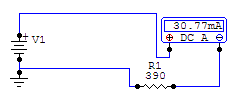
Here we have a resistance given as 390 ohms with 30.77 mA of current running through it. This time the resistance is already in the correct units. However, once again we have to convert the current, given in mA into amperes. 30.77 divided by 1000 equals a current of .03077 amperes.
These numbers are then put into the third variation of Ohm's Law which looks like this:
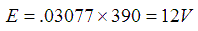
.03077 A times 390 ohms = 12 volts
Each formula is useful in a particular situation. You only need to know two of the three values of the variables in Ohm's Law to calculate the third.
Ohm's Law is very fundamental and someone working in the electronics field would be well served to commit all three variations to memory.