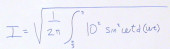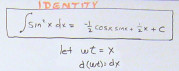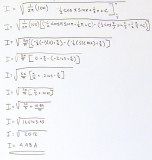2-4 RMS, or Effective, Currents and Voltages
- The equations we have been studying are usable where the waveform under consideration is sinusoidal. However, they do not permit the interpretation of the relative effectiveness of these waves vs. those with a different waveform. For a meaningful comparison to be made, we need another measurement tool with which we can judge differing waveforms on the same basis.
- What we need is something quantifiable produced by current and voltage that is measurable in any circuit carrying any waveform. A usable effect is the heating produced as current flows through a resistance.
- A DC circuit has a power expenditure in a resistance generated as heat that is independent of time. It is calculated by the formula
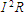 .
However, if the current
.
However, if the current  varies periodically
with time, the power loss becomes
varies periodically
with time, the power loss becomes 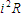 , which
is a function of time. With time now involved, to make the comparison we need to calculate the average
heating power of the current over a cycle.
, which
is a function of time. With time now involved, to make the comparison we need to calculate the average
heating power of the current over a cycle. - To calculate the average power over a cycle we need to integrate over the cycle the power loss equation for instantaneous power.
- Then that average power must be compared to the heating value of a DC circuit,
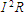 .
If we divide each of these two equations by
.
If we divide each of these two equations by 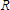 and then take
the square root of each side we see that
and then take
the square root of each side we see that 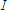 is equal to
is equal to
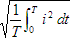 .
. - This gives us the equation
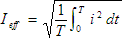 that allows the calculation of the effective heating value of the periodic current in terms of its DC counterpart.
that allows the calculation of the effective heating value of the periodic current in terms of its DC counterpart. - For a sinusoidal wave this same formula for the effective value is
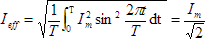
- The end result of this is to show that since the main purpose of any electric circuit is to transfer power and energy, RMS, Root Mean Square is the ultimate tool used as it facilitates accurate comparisons to be made of the relative effectiveness of different circuits with potentially differing currents.
- RMS is the way that voltages and currents are most commonly represented in literature and is the most common format by which measuring instruments present their values.
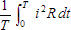 .
.
The best way to explain this is to look at an example. We will use the example 2-4 taken from the book. However, we will go into a lot more detail than they do to show how all the pieces covered so far fit together, first to set up the problem, then to show how the problem is solved.
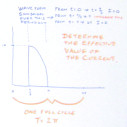
What we are given is that we have a periodic current, that is sinusoidal over the time that it flows. But it does not flow during all parts of its cycle.
We can see that we have a time frame from
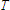 = 0 to
= 0 to
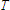 =
= 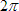 .
The current actually flows only from
.
The current actually flows only from 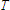 =
=
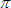 /3 to
/3 to
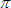 . The current has a maximum value
of 10
. The current has a maximum value
of 10 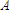 .
We are asked to calculate the effective current over the entire cycle of time of
.
We are asked to calculate the effective current over the entire cycle of time of 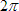 that equates to this periodic current.
that equates to this periodic current.
We will start by looking at the equations described above to see how we set this up to solve it. The graphic, when clicked will enlarge to show all the calculations.
First we start with the definition for how to calculate the average power.
Then we show how the effective current may be derived from this.
The instantaneous current in the equation is replaced by another set of terms that is its equivalent.
And parts of that equivalent equation are then replaced by other equivalent pieces we have seen in this chapter.
When we are through, we have an equation that looks like this:
Here, what we are essentially saying is that we want to get the squared instantaneous current, sum that up over the the interval from
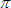 to
to
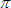 /3, then get its average by multiplying it
by 1 over the cycle time,
/3, then get its average by multiplying it
by 1 over the cycle time, 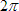 . Finally, the square root
of that number is to be derived to produce the answer.
. Finally, the square root
of that number is to be derived to produce the answer.
This book at this point summarily produces the answer 4.49
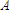 and
calls it done. (Oh yes, all the derivation of the formulas to get to their solution equation was also left up to the student to construct.)
and
calls it done. (Oh yes, all the derivation of the formulas to get to their solution equation was also left up to the student to construct.)
Well, I don't know about you, but my calculus is pretty rusty. Fortunately, I still have my handy "Calculus with Analytic Geometry" book by Earl Swokowski. (And I had to use it too!) Enough complaining, let's move on with solving this.
When we look at the base solution equation, we see a sin2 included. There must be a way to integrate that; and there is! I found the identity equation in Swokowski that you can see by clicking on the graphic to the left. Also in the graphic, you can see where I decided to try and simplify things a little by substituting "
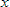 " for
" for 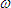
 .
.
Now to get to the meat of the problem. We have the framework set up, we basically just need to fill in the blanks. I am going to assume that even if your Calculus skills are as unexercised as mine, that you would not be reading this if you couldn't at least follow along with some algebra. I plugged the top and bottom parameters for our range
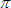 to
to
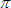 /3, and subtracted the second from the first
as we need to do. After simplification I got 4.48
/3, and subtracted the second from the first
as we need to do. After simplification I got 4.48 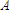 .
.
I hope that I have made this concept a little clearer in this page than the text made it to me. But then again, maybe the mental beating I took wasn't wasted effort. The harder you have to struggle with this stuff, the better you understand it.