Chapter 2-3 Purely Resistive AC Circuits
- Resistance is defined as a parameter that causes a voltage drop directly proportional to
the current that passes through it. That property is expressed as Ohm's Law. This effect holds equally true for both
direct current (DC) circuits and for alternating current (AC or time varying) circuits.
- We earlier defined an instantaneous current to be
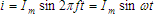 where
where  is the instantaneous current at any time is the instantaneous current at any time
 and
and 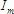 is the maximum value or amplitude. The quantity
is the maximum value or amplitude. The quantity
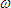 is expressed in radians per second and is the angular velocity. When that current exists in a simple series circuit the instantaneous voltage
is expressed in radians per second and is the angular velocity. When that current exists in a simple series circuit the instantaneous voltage
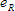 across the resistance is across the resistance is
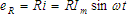 . .
- In a purely resistive circuit voltage and current are in phase. This is indicated on a graph by showing the curves crossing
the x-axis at the same points. For convenience of calculations, most often the origin is arbitrarily chosen as one of the crossing points.
The equations just presented imply that condition.
- However, a different time origin is often necessary for many calculations. Given here that we consider the current to have a phase angle
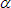 , these equations will look like this: , these equations will look like this:
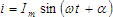 and and
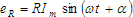 .
That will cause the peak voltage to be .
That will cause the peak voltage to be 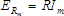 . .
|
|
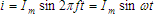 where
where  is the instantaneous current at any time
is the instantaneous current at any time
 and
and 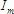 is the maximum value or amplitude. The quantity
is the maximum value or amplitude. The quantity
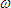 is expressed in radians per second and is the angular velocity. When that current exists in a simple series circuit the instantaneous voltage
is expressed in radians per second and is the angular velocity. When that current exists in a simple series circuit the instantaneous voltage
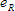 across the resistance is
across the resistance is
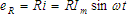 .
.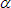 , these equations will look like this:
, these equations will look like this:
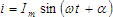 and
and
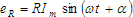 .
That will cause the peak voltage to be
.
That will cause the peak voltage to be 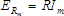 .
.