Chapter 1-4 Fundamental Circuit Laws; Kirchhoff's Laws
Kirchhoff's Laws provide a systematic way to study, understand and analyze basic electric circuits. They follow naturally given the properties we have discussed in the previous three sections. There are two such laws. The first one is:
- 1. The algebraic sum of all the currents directed toward a junction are equal to zero.
In other words, some currents may flow to a junction node, and some may flow from that same node, but in total no current will be left unaccounted for when you consider the directions of flows of each current and algebraically add them. Every ampere of current going in to a node will be matched by the same amount of current leaving the node.
As current flows through a circuit and encounters a node, the current will branch off down the various paths leaving the node. The amounts of current that flow down the different branches is based upon the relative resistances of the branches.
Let's look at a simple illustration. Here we have a circuit with 20
 of resistance in total and a 30
of resistance in total and a 30  source. By Ohm's Law
we can calculate that there ought to be 1.5
source. By Ohm's Law
we can calculate that there ought to be 1.5  of
current.
of
current.
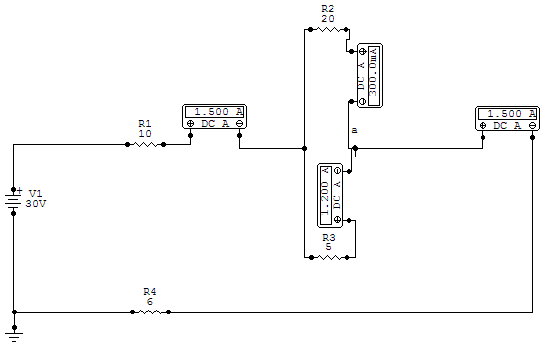
And indeed there is as we see just past R1 where we inserted an ammeter. But what happens when we come to the node where R2 and R3 branch off from the main circuit? R2 is a 20
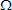 resistance
and R3 is a 5
resistance
and R3 is a 5 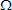 resistance. The total current splits into two
parts. And the split is based upon the relative resistance of the two branches.
resistance. The total current splits into two
parts. And the split is based upon the relative resistance of the two branches.
We can look at the next two ammeters, respectively in series with R2 and R3. We see that the higher resistance of R2 allows only .3
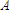 of current to flow. And the lower resistance in R3
allows 1.2
of current to flow. And the lower resistance in R3
allows 1.2 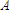 . The sum of .3
. The sum of .3
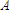 and 1.2
and 1.2
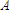 equals the total
1.5
equals the total
1.5 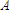 sent in to the parallelled resistors.
sent in to the parallelled resistors.
Once the currents pass through the resistors in parallel, they recombine at terminal
 and continue around the circuit. The fourth ammeter in the circuit registers 1.5
and continue around the circuit. The fourth ammeter in the circuit registers 1.5 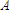 ,
showing that all current that entered the dual branches of the parallel resistors also left them, and sums to the original total.
,
showing that all current that entered the dual branches of the parallel resistors also left them, and sums to the original total.
Now we come to the second of Kirchhoff's laws:
- 2. The algebraic sum of all the voltage drops around a closed circuit is zero.
- Voltage drops across resistances are always in the same direction as the circuit current flow.
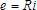 Voltage equals the product of the current and resistance. When a current passes through a resistance,
energy transfer is effected. This energy transfer is known as Work. Evidence of this work having been done
is the potential difference across the two sides of the resistance.
Voltage equals the product of the current and resistance. When a current passes through a resistance,
energy transfer is effected. This energy transfer is known as Work. Evidence of this work having been done
is the potential difference across the two sides of the resistance.
Another way of saying this is that there is a voltage drop across the resistance. Since the current has to pass through the resistance to cause work to occur, then (relative to a fixed reference point) the voltage will be higher on the side of the resistance where the current enters than on the side where it exits.
- Voltage rises (or drops) across sources are always in the same direction, but are accounted for based upon the direction that the circuit path is followed.
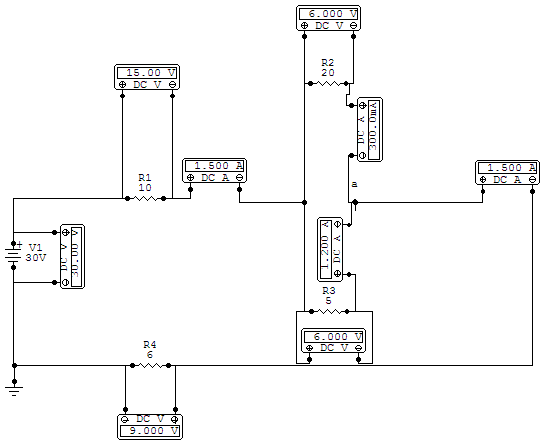
We put a voltmeter across each resistance and across the source. We have the current going clockwise in this circuit. Therefore, there should be a voltage drop across each resistance. And there is. Note the polarity of the voltmeters across the resistances. What they are measuring is the voltage at the positive terminal (where the current enters) of each resistance in relation to the voltage at the negative terminal. The voltage is always higher where the current enters, so the meters are registering voltage drops.
The voltage across the source is a voltage rise from negative to positive. It is exactly opposite in sign but equal in magnitude to the combined voltage drops of the resistances in the circuit. Going around the circuit we have 30
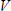 -15
-15 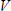 -6
-6 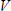 -9
-9 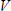 = 0
= 0 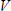 , which
is exactly what we should have to prove Kirchhoff's second law.
, which
is exactly what we should have to prove Kirchhoff's second law.