Chapter 1-3 : Resistance; Ohm's Law
- Resistance is the element of circuits that has a voltage across it proportional to the current passing through it.
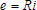 (Ohm's Law)
(Ohm's Law)
where
 = potential in volts,
= potential in volts,
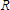 = resistance in ohms, and
= resistance in ohms, and
 = current in amperes.
= current in amperes.
The proportionality constant in this equation relating voltage and current is resistance.
- Energy dissipated overcoming resistance will be observed as heat.
- An electric charge gives up energy as it passes through a resistance, creating heat. This may be measured as a voltage drop in the direction of the current. This is a decrease in potential.
- Power dissipated by the resistance is the energy loss over time.
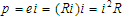
where
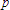 = power in watts.
= power in watts.
Looking back to the first section we can see the relationship:
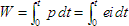
which describes power over time in watt-secs or joules.
- The resistance of a conductor is directly proportional to its length, inversely proportional to its cross-sectional area, and is a function of the material from which it is made.
- Resistivity is defined as the resistance of a volume of unit cross section and unit length. Even though it is not MKS system based, we often see the unit of length represented as the foot and the unit of cross-sectional area represented as the mil.
- A circular mil is the area of a circle 1 mil (1/1000") in diameter. When the conductor's diameter in mils is squared, it yields the area in circular mils.
- The unit of resistivity then, is the ohm-circular mil per foot.
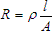
where
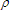 = resistivity in ohms,
= resistivity in ohms,
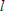 = length, and
= length, and
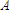 = area. (Use any consistent units of measure.)
= area. (Use any consistent units of measure.)
- Resistance is also affected by the temperature of the material. The change in resistance is related to the change in temperature in degrees Celsius and the temperature coefficient of the material measured at the base temperature.
![R sub2 = R sub 1 [1 + alpha sub1 (t sub 2 - t sub 1)]](http://prismglow.com/electronics/eees/ch01/ch1_3/r2eqr1xtmpcoef.gif)
where
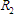 is the resistance at time 2,
is the resistance at time 2,
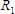 is the resistance at time 1,
is the resistance at time 1,
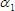 is the temperature coefficient of the material at time 1,
is the temperature coefficient of the material at time 1,
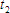 is the temperature in degrees Celsius at time 2, and
is the temperature in degrees Celsius at time 2, and
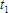 is the temperature in degrees Celsius at time 1.
is the temperature in degrees Celsius at time 1.A more convenient, but material specific formula that can be used for standard annealed copper is:
![R sub 2 = R sub 1 [(234.5 + t sub 2) / (234.5 + t sub1)]](http://prismglow.com/electronics/eees/ch01/ch1_3/r2eqr1-cop.gif)