Li'l Hindy
Hydrogen Balloon and Radio Antenna
This was a multi-purpose experiment. The seed of the idea started when we thought about lifting a temporary full wave receiving antenna for an AM radio station by using a hydrogen balloon. The antenna would consist of nothing more than a thin wire, but would have the proper length of one full wavelength of the target radio station frequency. That could not be achieved by running the wire horizontally due to lack of real estate.
Objectives
- Determine the length of antenna and the mass of wire that would be required.
- Test a couple of different balloons' size, mass and lift to determine required capacity.
- Calculate the hypothetical amounts of zinc and hydrochloric acid required to fill the balloons with hydrogen.
- Measure carefully enough the starting reactants such that we could predict the quantities of the resultants with some degree of accuracy.
What Length Antenna?
The radio station frequency of interest was 740 kHz. To start with, we needed to know what wavelength corresponded to that frequency. The equation for this calculation is: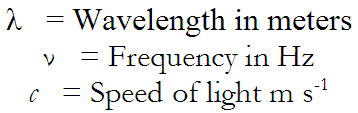
Plugging in the numbers, we get:
The wire we had available for the antenna is 27 AWG copper. Per the "Wire Table, Standard Annealed Copper - American Wire Gauge (B & S) English Units", 27 AWG wire has a mass of .9078 kilograms per kilometer. With 405 m of wire needed, the total mass of wire would be .368 kg. Perhaps more importantly, the 27 AWG wire has resistance of 5.922 meters per ohm at 20°C. This works out to a total resistance of 68.4 ohms.
Before we would ever actually try to lift a wire of this gauge, we need to determine if the large resistance would offset any gain to be had from the length. However, this question does not prevent us from continuing with the experiment.
Balloon Sizes and Volumes
We had two sizes of balloons handy that we could use. Per the package labels, the claims were that one would grow to 7" diameter and one would expand to 12". We weighed them and found the smaller balloon had a mass of 1.3 g and the larger one 2.8 g.Assuming spherically shaped balloons when fully inflated, we calculated the volumes for each size:
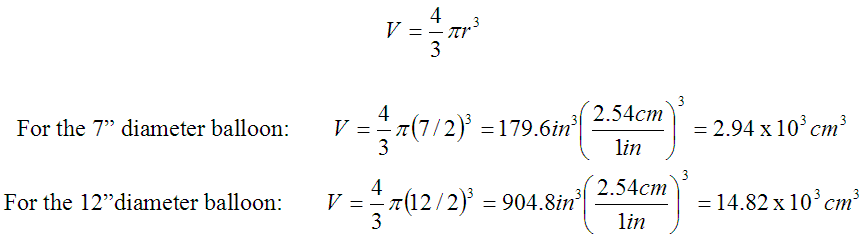
Lift of Hydrogen Gas
Now we needed to know how much lift a given volume of hydrogen would produce. First we had to understand what lift actually is. All that is really happening when a balloon rises is that the volume of hydrogen inside the balloon has less mass than the volume of air it is displacing. It, therefore, wants to rise. So we calculate the relative masses of air and hydrogen that would apply to these two balloon sizes.Air's mass is calculated by getting a weighted average of the N2 and O2 components.
| Component | Percentage | Atomic Mass g mol -1 | No. Atoms | Component Mass |
| Nitrogen | 79% | 14.007 | 2 | 22.13 g mol -1 |
| Oxygen | 21% | 15.999 | 2 | 6.72 g mol -1 |
| Air | 28.85 g mol -1 |
Hydrogen is simpler as there is no weighting. We do need to remember that it is diatomic though, just as are nitrogen and oxygen.
| Component | Percentage | Atomic Mass g mol -1 | No. Atoms | Component Mass |
| Hydrogen | 100% | 1.0797 | 2 | 2.016 g mol -1 |
| Hydrogen (H2) | 2.016 g mol -1 |
If we now subtract the mass of the hydrogen from the mass of the air, we get the net lift.
Air mass 28.85 g mol-1 - Hydrogen mass 2.016 g mol-1 = 26.83 g mol-1 lift.
Balloons' Lift Capabilities
There are 22.4 liters of gas in one mole of any gas (at standard conditions). The smaller balloon would hold 2.94 liters. That is 13.1% of a mole. The larger balloon would hold 14.28 liters. That is 63.8 % of a mole. With those factors and the mass of each balloon taken into consideration, we could calculate the net lifts.| Balloon Diameter | Balloon Mass | Lift from Gas | Payload Maximum |
| 7" | 1.3 g | 3.5 g | 2.2 g |
| 12" | 2.8 g | 17.8 g | 15 g |
With the understanding that neither balloon by itself would come close to lifting .368 kg, we chose the smaller one with which to work. As the process of hydrogen generation was not yet clearly understood and we did want to have enough gas to get some lift such that we could measure it, we started small. Also, as hydrogen is quite flammable, we did not want to generate more gas than we really needed.
Chemistry
Now that we had scoped the amount of hydrogen we would need, we needed to determine the quantities of starting reactants required to generate that gas volume. We chose to generate hydrogen by reacting zinc metal with hydrochloric acid. The balanced equation looks like this: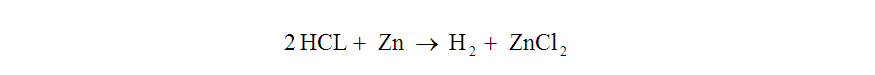
This means that two moles of hydrogen chloride will react with one mole of zinc to yield one mole of diatomic hydrogen and one mole of zinc chloride.
The first step was to calculate out the molar masses for all the reactants and for the resulting products.
Reactants:
| Element | Atomic Weight (g mol-1) |
| Hydrogen | 1.0079 |
| Chlorine | 35.45 |
| Zinc | 65.35 |
Hydrogen Chloride (HCl)
| Component | Atomic Mass (g mol-1) | No. Atoms | Comp Mass |
| Hydrogen | 1.00797 | 1 | 1.00797 g mol-1 |
| Chlorine | 35.45 | 1 | 35.45 g mol-1 |
| Hydrogen Chloride | 36.46 g mol-1 |
Zinc Chloride
| Component | Atomic Mass (g mol-1) | No. Atoms | Comp Mass | Comp % Mass |
| Zinc | 65.45 | 1 | 65.45 g mol-1 | 48% |
| Chlorine | 35.45 | 2 | 70.90 g mol-1 | 52% |
| Zinc Chloride | 136.25 g mol-1 | 100% |
The volume of H2 needed to fill the small balloon (according to the initial calculations) was 2.94 liters or 13.1% mol. That would force the balanced equation into the following form:
Zinc is easy enough to put on a scale to find its mass. But the second reactant is HCl which we had in the form of a 31.45% solution of hydrochloric acid. We had to determine a way to measure the correct number of moles of HCl volumetrically.
The HCl solution has a molarity of 10. (It was incorrectly assumed in the experimental work that this was 12 molar. It will be seen that we end up with an excess of zinc reactant due to this mistake.) To get .262 moles of HCl then would require
.262 mol HCL x 1 000 ml x 10 mol-1 = 26.2 ml 31.45% HCl solution
And the amount of zinc necessary to react with .262 moles 31.45% HCl solution would be:
.131 mol Zn x 65.35 g mol-1 = 8.56 g Zn
Reaction Calculations - Pro Forma
However, as stated earlier, the molarity of the HCl was overestimated and as such, the quantity of the acid was less than needed for a complete reaction. Additionally, the amount of zinc used was larger than the calculated needed amount. The actual quantities reacted were:
31.45% HCl solution: 25.0 ml
Zinc metal: 9.6 g
The 31.45% HCl solution was the limiting reactant in this setup and there was zinc left over at completion.
The equation that would fit these quantities, assuming 100% reaction to completion would be:
Zinc metal: 9.6 g
Theoretically there should be 9.6 g Zn - (.125 mol Zn * 65.35 g mol-1) = 1.4 g Zn remaining.
The Actual Reaction
We used a 25mm x 150 mm test tube with a volume of approximately 75 ml. Into this test tube, we put 9.6 g Zn that was cut from a sacrificial anode in 3 irregularly sized pieces. Then we poured 25 ml of HCl over the Zn pieces. Immediately a strong reaction occurred and hydrogen rapidly began to evolve from the zinc and exit the mouth of the test tube. The method used to collect the hydrogen was to place a balloon over the mouth of the test tube as soon as the reaction started. (A better idea would have been to use a cork with a hole and a glass tube with the balloon already attached.) As it was, we lost about 15 seconds worth of evolved gas while trying to get the balloon into place.The reaction generated a great amount of heat.

As the reaction had not totally stopped, we decided to let it continue to see how long it would continue and then to attempt to recover the ZnCl2 which would be one of the resulting products. We pulled another small balloon over the mouth and set the test tube aside for the reaction to finish.
The balloon was capable of floating, but it contained less than its full capacity. At its widest point, it was approximately 12 cm across. It had a length from top to the tie-off point of approximately 20 cm.

We attached various weights to the thread to see how much mass would just offset the lift. The correct balancing mass was 0.3 g. This when added to the 1.3 g mass of the empty balloon yielded 1.6 g of lift. 1.6 g H2 lift power / 26.83 g mol-1 lift factor = 6.0% mol H2. Clearly, we had both lost some of the hydrogen initially and not all the hydrogen that would be generated had been collected. (Hydrogen atoms are so small and escape so rapidly through a rubber balloon that one cannot wait too long to measure what one must. The generation of hydrogen had slowed to the point where the balloon was not going to get any bigger.)
Theoretical vs. Measured Ending Reactants and Products
The evolution of hydrogen continued at an ever decreasing rate for 5 more days. The second balloon never inflated much past the point of simply standing up. We knew that an exact hydrogen measurement would not be possible, but we did want to see how closely we could determine the final quantity of ZnCl2. And we could see that there still was some zinc metal left unreacted, unexpected at the time.When we removed the second balloon, there was 23 ml of solution remaining and 2.2 g of Zn. When we weighed the liquid, we determined it had a mass of 33.3 g. Before we worked to evaporate the liquid to recover the dissolved ZnCl2 we calculated what the theoretical amount should be based upon the missing zinc that had gone into the reaction. 9.6 g of zinc to start, less 2.2 g at the end indicated that 7.4 g of zinc had reacted. As 48% by weight of ZnCl2 is zinc, the remaining 52% is chlorine. This gave a theoretical expected mass of 15.4 g of ZnCl2.
Upon evaporation of the liquid through heating, we obtained a measured mass of 15.7 g of ZnCl2. This was an approximate 1.9% measurement difference.
Working backwards through the calculations, 15.7g ZnCl2 divided by 136.25 g mol-1 for the compound indicates 11.5% mol. Continuing with that mol percentage and plugging it into the known balanced equation, we get the following:
Since we started with .250 mol of HCl there must have been 0.02 mol HCl remaining in the liquid we evaporated. That is less than .73 g. (However, it seems a reasonable explanation for the tiny amount of hydrogen that was still coming from the zinc after sitting for the 5 days.) The HCl would have left as a gas at the same time as the water vapor.
0.115 mol Zn is 7.5 g. Since we were working with a scale of 0.1 g accuracy and it showed we had reacted 7.4 g of zinc, this too at 1.5% measurement difference was understandable. We could directly account for only .06 moles of hydrogen. However, with the other measurements tying out as they do, we expect our hypothesis about the initial burst of activity when we poured the HCl on the Zn and the commensurate loss of some hydrogen would account for most of the difference.
Conclusion
We are not likely to pursue the raising of an antenna by this particular method. First, it would take about 25 - 12" diameter balloons filled completely with hydrogen to lift the wire the needed 405 m. The quantity of H2 required is approximately 16.6 moles. 368 g/15 g balloon-1 = 24.5 (25 full) balloons. That is 16.6 * 65.35 g = 1 085 g Zn and 1 660 ml 31.45% HCl (10 M) solution. We do not believe we could fill the 25 balloons quickly enough to achieve the required height prior to the hydrogen's not so slow exodus through their rubber skins. We would have to use somewhat larger quantities of reactants than this in practice as the reaction slows markedly well before going to completion.The intent of this idea was to send up a wire attached to a balloon that would be inconspicuous. 25 - 1 foot diameter balloons in a bunch are far from inconspicuous and might call unwelcome attention to our experiment. It could also be interpreted as something other than what it was designed to be, due to the current mood of society. Along with that is the fact that the time when we try this would need to be practically windless so that the path of the wire would be up and not across the trees or power lines.
Li'l Hindy

May 2, 2010